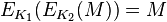我们开展的DRKCTF！

没打，而且好难，所以跟着wp把它复现出来

CRYPTO

密码_sinin

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
from Crypto.Util.number import *

m = b'flag{********}'
a =  getPrime(247)
b =  getPrime(247)
n =  getPrime(247)

seed = bytes_to_long(m)

class LCG:
    def __init__(self, seed, a, b, m):
        self.seed = seed  
        self.a = a  
        self.b = b  
        self.m = m  

    def generate(self):
        self.seed = (self.a * self.seed + self.b) % self.m
        self.seed = (self.a * self.seed + self.b) % self.m
        return self.seed

seed = bytes_to_long(m)

output = LCG(seed,a,b,n)

for i in range(getPrime(16)):
    output.generate()

print(output.generate())
print(output.generate())
print(output.generate())
print(output.generate())
print(output.generate())

'''
5944442525761903973219225838876172353829065175803203250803344015146870499
141002272698398325287408425994092371191022957387708398440724215884974524650
42216026849704835847606250691811468183437263898865832489347515649912153042
67696624031762373831757634064133996220332196053248058707361437259689848885
19724224939085795542564952999993739673429585489399516522926780014664745253
'''

这个是LCG线性同余随机数生成器

原理是攻击线性同余生成器(LCG) (zer0yu.github.io)

过程：

  1. 求m
  2. 求a
  3. 求b
  4. 求seed

这里由于是间隔一个来给X，所以求到$a^2$之后不好求a，太大了，所以要以$a^2$作为新的a，$(a+1)b$作为新的b

求到后就可以穷举2的16次方爆flag

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import math
import gmpy2 as gy
x0 = 5944442525761903973219225838876172353829065175803203250803344015146870499
x1 = 141002272698398325287408425994092371191022957387708398440724215884974524650
x2 = 42216026849704835847606250691811468183437263898865832489347515649912153042
x3 = 67696624031762373831757634064133996220332196053248058707361437259689848885
x4 = 19724224939085795542564952999993739673429585489399516522926780014664745253

d0 = x1 - x0
d1 = x2 - x1
d2 = x3 - x2
d3 = x4 - x3

k1 = d2*d0 - d1*d1
k2 = d3*d0 - d1*d2
m = math.gcd(k1,k2)
print(m)
inv_d0 = gy.invert(d0,m)
pa = d1*inv_d0 % m
print(pa)

b = x1 - pa*x0 % m
inv_a = gy.invert(pa,m)
seed = inv_a * (x0-b)%m
for i in range(2**16):
    seed = inv_a * (seed-b)% m
    flag = long_to_bytes(seed)
    if b'flag' in flag:
        print(flag)
 #b'flag{Hello_CTF}'

还有第二种方法

Grobner基求解多项式多个根，但是不会，给个D神的链接QAQ

LCG | DexterJie’Blog

EzDES

一开始没想到QAQ

DES 弱密钥 - lightless blog看看佬的blog

有四个弱密钥是绝对不能使用的：

1
2
3
4
\x01\x01\x01\x01\x01\x01\x01\x01
\xFE\xFE\xFE\xFE\xFE\xFE\xFE\xFE
\xE0\xE0\xE0\xE0\xF1\xF1\xF1\xF1
\x1F\x1F\x1F\x1F\x0E\x0E\x0E\x0E

如果不考虑校验位的密钥，下面几个也是属于弱密钥的：

1
2
3
4
\x00\x00\x00\x00\x00\x00\x00\x00
\xFF\xFF\xFF\xFF\xFF\xFF\xFF\xFF
\xE1\xE1\xE1\xE1\xF0\xF0\xF0\xF0
\x1E\x1E\x1E\x1E\x0F\x0F\x0F\x0F

如果使用弱密钥，PC1 计算的结果会导致轮密钥全部为 0，全部为 1 或全部 01 交替。
因为所有的轮密钥都是一样的，并且 DES 是 Feistel 网络的结构，这就导致加密函数是自反相 (self-inverting) 的，结果就是加密一次看起来没什么问题，但是如果再加密一次就得到了明文。

部分弱密钥

部分弱密钥是指只会在计算过程中产生两个不同的子密钥，每一个在加密的过程中使用 8 次。这就意味着这对密钥 K1 和 K2 有如下性质：
部分弱密钥性质

6 个常见的部分弱密钥对

  • 0x011F011F010E010E and 0x1F011F010E010E01
  • 0x01E001E001F101F1 and 0xE001E001F101F101
  • 0x01FE01FE01FE01FE and 0xFE01FE01FE01FE01
  • 0x1FE01FE00EF10EF1 and 0xE01FE01FF10EF10E
  • 0x1FFE1FFE0EFE0EFE and 0xFE1FFE1FFE0EFE0E
  • 0xE0FEE0FEF1FEF1FE and 0xFEE0FEE0FEF1FEF1

OpenSSL 中对弱密钥的检查

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
119 static const DES_cblock weak_keys[NUM_WEAK_KEY]={
120     /* weak keys */
121     {0x01,0x01,0x01,0x01,0x01,0x01,0x01,0x01},
122     {0xFE,0xFE,0xFE,0xFE,0xFE,0xFE,0xFE,0xFE},
123     {0x1F,0x1F,0x1F,0x1F,0x0E,0x0E,0x0E,0x0E},
124     {0xE0,0xE0,0xE0,0xE0,0xF1,0xF1,0xF1,0xF1},
125     /* semi-weak keys */
126     {0x01,0xFE,0x01,0xFE,0x01,0xFE,0x01,0xFE},
127     {0xFE,0x01,0xFE,0x01,0xFE,0x01,0xFE,0x01},
128     {0x1F,0xE0,0x1F,0xE0,0x0E,0xF1,0x0E,0xF1},
129     {0xE0,0x1F,0xE0,0x1F,0xF1,0x0E,0xF1,0x0E},
130     {0x01,0xE0,0x01,0xE0,0x01,0xF1,0x01,0xF1},
131     {0xE0,0x01,0xE0,0x01,0xF1,0x01,0xF1,0x01},
132     {0x1F,0xFE,0x1F,0xFE,0x0E,0xFE,0x0E,0xFE},
133     {0xFE,0x1F,0xFE,0x1F,0xFE,0x0E,0xFE,0x0E},
134     {0x01,0x1F,0x01,0x1F,0x01,0x0E,0x01,0x0E},
135     {0x1F,0x01,0x1F,0x01,0x0E,0x01,0x0E,0x01},
136     {0xE0,0xFE,0xE0,0xFE,0xF1,0xFE,0xF1,0xFE},
137     {0xFE,0xE0,0xFE,0xE0,0xFE,0xF1,0xFE,0xF1}};

有弱密钥的加密算法

  • DES
  • RC4
  • IDEA
  • Blowfish

摘抄完QAQ，再根据提示

二次加密得到明文

1
2
3
4
5
6
7
8
9
10
11
from Crypto.Cipher import DES
from Crypto.Util.Padding import pad

flag = b't\xe4f\x19\xc6\xef\xaaL\xc3R}\x08;K\xc9\x88\xa6|\nF\xc3\x12h\xcd\xd3x\xc3(\x91\x08\x841\xca\x8b\xc1\x94\xb5\x9f[\xcd\xc6\x9f\xf9\xf6\xca\xf5\x1a\xda\x16\xcf\x89\x154\xa1\xfe\xc5\x16\xcf\x89\x154\xa1\xfe\xc5'
key = '0101010101010101'
key = bytes.fromhex(key)
des = DES.new(key, DES.MODE_ECB)

enc = des.encrypt(pad(flag,64))
print(enc[:enc.find(b'}')+1])
#b'DRKCTF{We4k_K3y_1s_V3ry_D4nger0us_In_DES}'

MidRSA

这道题没写完

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
from Crypto.Util.number import *
from secret import flag
import random
import gmpy2

def generate_Key1(ebits):
    e = [getPrime(ebits) for _ in range(4)]
    return e

def encrypt1(message,e):
    n = gmpy2.next_prime(bytes_to_long(message) << 300)
    m = getPrime(256)
    c = [int(pow(m,e[i],n)) for i in range(len(e))]
    return c

def generate_Key2(nbits):
    p = getPrime(nbits // 2)
    q = getPrime(nbits // 2)
    n = p*q
    e = [random.getrandbits(nbits // 4) for _ in range(3)]
    return n,e

def encrypt2(message,e,n):
    m = bytes_to_long(message)
    c = [int(pow(m,e[i],n)) for i in range(len(e))]
    return c
    
assert flag.startswith(b"DRKCTF{")

flag1 = flag[:len(flag)//2]
flag2 = flag[len(flag)//2:]

ebits = 7
e1 = generate_Key1(ebits)
cipher1 = encrypt1(flag1,e1)
print("e1 =",e1)
print("cipher1 =",cipher1)

nbits = 1024
n,e2 = generate_Key2(nbits)
cipher2 = encrypt2(flag2,e2,n)
print("e2 =",e2)
print("cipher2 =",cipher2)
print("n =",n)

"""
e1 = [109, 71, 109, 73]
cipher1 = [36272047346364825234770733058042613197790911431212158822254782055957208837848605160852567043492625692783344073921185227328379941291979083011033, 13421582077901767047291741873622169312010984740586925881415103229648835151589774736786336965745532072099996467445790339749720696886313635920080, 36272047346364825234770733058042613197790911431212158822254782055957208837848605160852567043492625692783344073921185227328379941291979083011033, 41425183140413487232780768389488969603566343428250573532166425276868000949579663990819005141199597640625439816343697426958648927294289659127871]
e2 = [79572758141493570128961125255246129069540961757778793209698370333142346488381, 80555585862127636800866563977080055603517001358195529410497461746213789997225, 44651921320695090688745333790065512192118202496468714141526113242887125432380]
cipher2 = [58600444300331800249882073146233995912287198739549440714207984476331259754331716531491187240053630185776787152600165426285021284302994699108557023545574315706006132536588848833818758624067461985444940651823107522770906474037882323326792755635934081822967331031854184791299228513024491344725765476710816941057, 16511944800191885973496391252612222059697387587833308714567450121364756390806094606646424594583975159634952911600665271092389815248477961923357683297311169260578508157717777465241680062644118354471550223231057620392252324514411927096940875466794869671163453991620492008856178108060167556176019729800517994337, 80885008609388989196377721090246742575908473911131498982960117640742106565184297197238656375198284856442596226398287448931285735903463892735111244609358611618958293002176923706195402338331128766464276441210238388187625107435781170368017908610916585774514676482124401329575553658828115269495158818527164441546]
n = 93468142044831350317940409833603031534515663349871776634867176846669780024082517910566484997161088199091160371537367121403194814422867749777235397168852158723228851090445429617275680206703935781244466363279841409768649097588586494453125840436600639420286950914680651600232197982546122764845043227394567787283
"""

第一部分

这里有两个c，知道n是m<<300，只要找到模数n，就找到了m，构造$c_i=m^{e_i} \mod n$改写成${c_i}^{e_j}={{m^{e_i}}^{e_j}} ={c_j}^{e_i}\mod n$

这样两数之差就是kn，再来一个kn，求gcd即可

第二部分

这里重看一下共模攻击和CRT：

中国剩余定理(CRT)及其扩展(EXCRT)详解 - ailanxier - 博客园 (cnblogs.com)

这里要想到三个e对应三个方程，不能简单当成gcd(e1,e2,e3)

把它当成两次共模攻击

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# from prism import *
# from math import *
from Crypto.Util.number import *
from gmpy2 import *


e1 = [109, 71, 109, 73]
cipher1 = [36272047346364825234770733058042613197790911431212158822254782055957208837848605160852567043492625692783344073921185227328379941291979083011033, 13421582077901767047291741873622169312010984740586925881415103229648835151589774736786336965745532072099996467445790339749720696886313635920080, 36272047346364825234770733058042613197790911431212158822254782055957208837848605160852567043492625692783344073921185227328379941291979083011033, 41425183140413487232780768389488969603566343428250573532166425276868000949579663990819005141199597640625439816343697426958648927294289659127871]

d1 = cipher1[0]**e1[1] - cipher1[1]**e1[0]
d2 = cipher1[2]**e1[3] - cipher1[3]**e1[2]

n = gcd(d1,d2)

m1 = n>>300
# print(long_to_bytes(m1))


e2 = [79572758141493570128961125255246129069540961757778793209698370333142346488381, 80555585862127636800866563977080055603517001358195529410497461746213789997225, 44651921320695090688745333790065512192118202496468714141526113242887125432380]
c2 = [58600444300331800249882073146233995912287198739549440714207984476331259754331716531491187240053630185776787152600165426285021284302994699108557023545574315706006132536588848833818758624067461985444940651823107522770906474037882323326792755635934081822967331031854184791299228513024491344725765476710816941057, 16511944800191885973496391252612222059697387587833308714567450121364756390806094606646424594583975159634952911600665271092389815248477961923357683297311169260578508157717777465241680062644118354471550223231057620392252324514411927096940875466794869671163453991620492008856178108060167556176019729800517994337, 80885008609388989196377721090246742575908473911131498982960117640742106565184297197238656375198284856442596226398287448931285735903463892735111244609358611618958293002176923706195402338331128766464276441210238388187625107435781170368017908610916585774514676482124401329575553658828115269495158818527164441546]
n = 93468142044831350317940409833603031534515663349871776634867176846669780024082517910566484997161088199091160371537367121403194814422867749777235397168852158723228851090445429617275680206703935781244466363279841409768649097588586494453125840436600639420286950914680651600232197982546122764845043227394567787283
def egcd(a, b):
  if a == 0:
    return (b, 0, 1)
  else:
    g, y, x = egcd(b % a, a)
    return (g, x - (b // a) * y, y)
def modinv(a, m):
  g, x, y = egcd(a, m)
  if g != 1:
    raise Exception('modular inverse does not exist')
  else:
    return x % m

_,s1, s2 = gmpy2.gcdext(e2[0],e2[1])
# print(s)
if s1<0:
    s1 = - s1
    c2[0] = modinv(c2[0], n)
elif s2<0:
    s2 = - s2
    c2[1] = modinv(c2[1], n)
# print(t)
m2 = pow(c2[0], s1, n) * pow(c2[1], s2, n) % n

print(long_to_bytes(m1)+long_to_bytes(m2))
#b'DRKCTF{5d0b96e8-e069-4378-82e7-120e4b761a0b}'

REVERSE

elec_go

佬出的题，第一次见

根据

Electron编写的exe 逆向思路 - 『脱壳破解区』 - 吾爱破解 - LCG - LSG |安卓破解|病毒分析|www.52pojie.cn

1
2
3
4
npm install asar -g
cd apps
asar extract app.asar app //解压拿到源码
asar pack app app.asar //重新打包

打开js源代码，有一个base64，解密之后发现是aes，但是不知道key，直接写一个

1
2
3
4
  dialog.showMessageBox({
    message: `k3y 的值是：${k3y.toString()}`,
    buttons: ['OK']
})

重新打包，拿到key的值，在线解密

image-20240530225931951

flower_tea

在这里说一下出题思路吧QAQ

这个题本来是想考一下去花指令的，没想到有佬直接调出来了，tql

花指令基本都很萌新QAQ，对栈做操作或者call，ret。

想了一下，可能反调试比花出的还好一点。毕竟x64的和x86有一点不一样。

感觉还有可以改进的地方：

隐藏交叉引用-用多级指针来隐藏交叉引用
真tea中jmp修正为jz和jnz，这样能起到一些混淆的作用
防止附加调试-在scanf之后再次判断调试状态，修改hook

但是都不会QAQ，还是要好好学，下面抄的官方wp

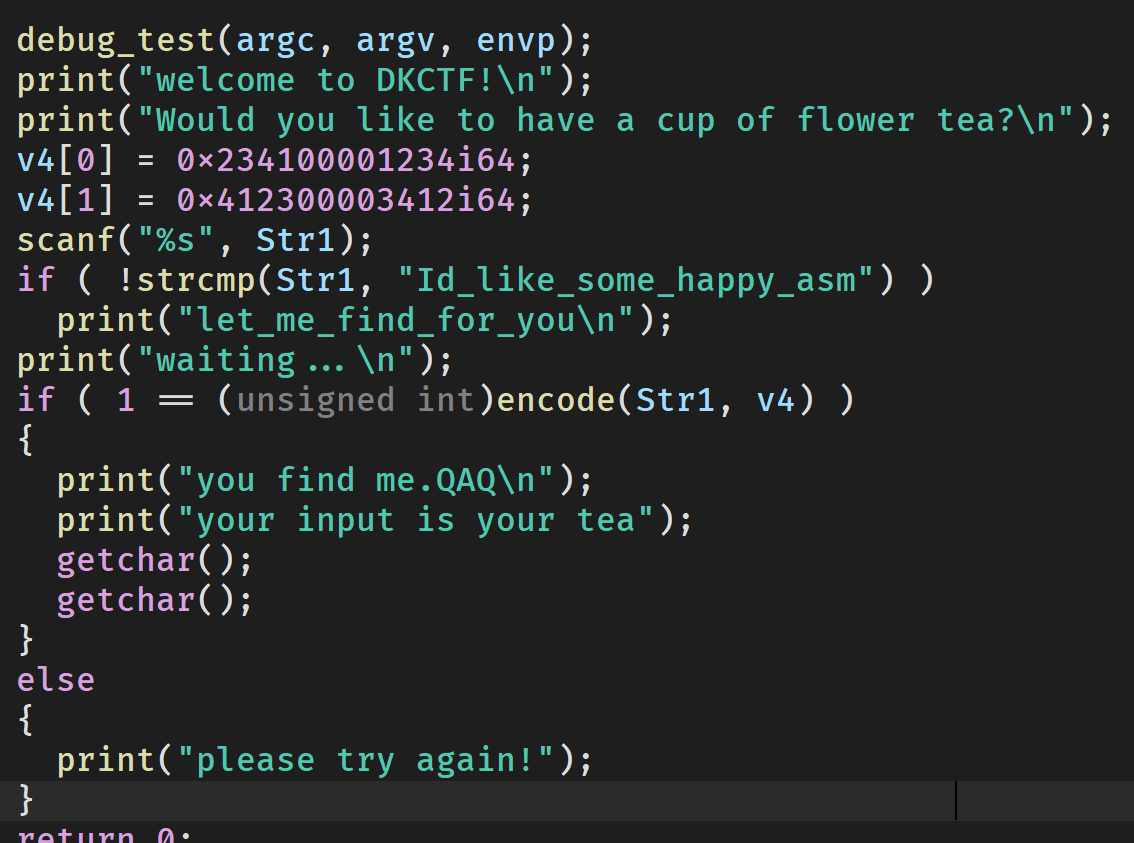
观察main函数：
主函数的大概是这样。
image.png
如果要调试，要先把第一个函数nop掉（实际上并不用）
这里先看encode函数，点开后是爆红的，所以先解花指令
image.png
这个是一个简单的jmp花指令，把后面的jmp nop掉，然后可以看到第一部分。
这时最上面还是有标红
在汇编界面看看哪里还有花
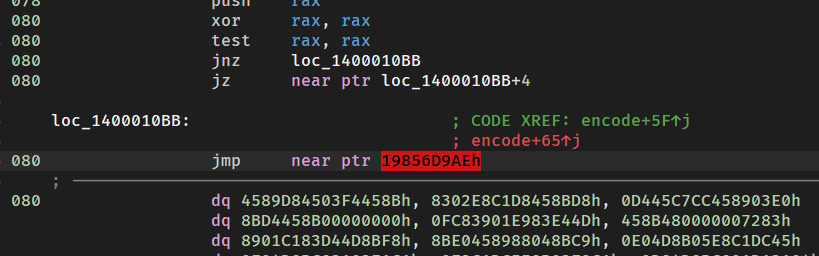
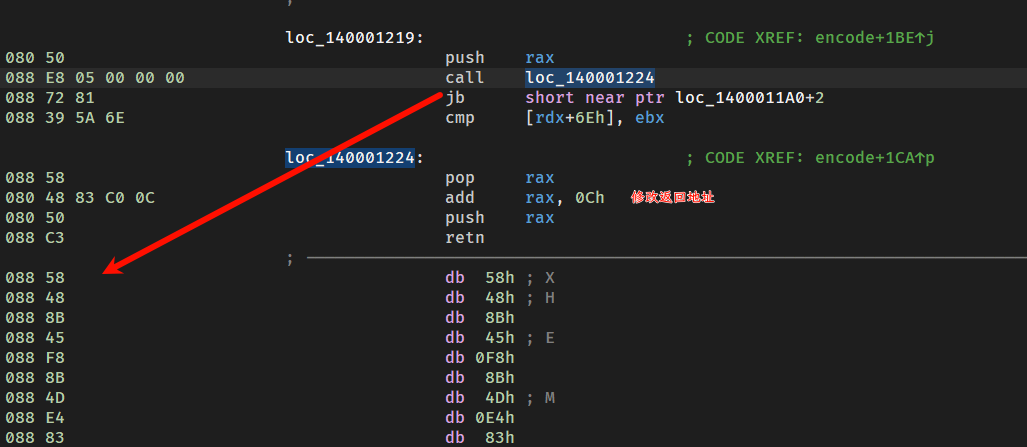
image.png
这里有一个奇怪的call：
逻辑是：call完之后把ret的值+0xC然后返回
把这一部分按u解除，在加0xC后的位置再反编译
image.png
所以ret之后就会到pop的位置
把中间这一段全部nop，然后把整个函数u，然后c，再浏览一下函数，中间有一个怪jmp，删掉
image.png
然后再p，得到解完花的函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
__int64 __fastcall encode(__int64 a1, __int64 a2)
{
  __int64 v2; // rcx
  int v3; // eax
  bool v4; // zf
  int v5; // eax
  int v7; // [rsp+2Ch] [rbp-34h]
  int v8; // [rsp+30h] [rbp-30h]
  unsigned int i; // [rsp+34h] [rbp-2Ch]
  unsigned int v10; // [rsp+38h] [rbp-28h]
  unsigned int v11; // [rsp+3Ch] [rbp-24h]
  unsigned int v12; // [rsp+40h] [rbp-20h]
  int v13; // [rsp+44h] [rbp-1Ch]
  _BYTE v15[12]; // [rsp+54h] [rbp-Ch]

  *(_QWORD *)&v15[4] = a1;
  *(_DWORD *)v15 = 0x9E3779B9;
  v8 = 9;
  v10 = 0;
  v11 = *(_DWORD *)(a1 + 56);
  do
  {
    v10 -= 0x61C88647;
    v7 = (v10 >> 2) & 3;
    for ( i = 0; ; ++i )
    {
      v2 = 14i64;
      if ( i >= 0xE )
        break;
      v12 = *(_DWORD *)(*(_QWORD *)&v15[4] + 4i64 * (i + 1));
      v3 = *(_DWORD *)(*(_QWORD *)&v15[4] + 4i64 * i)
         + (((v11 ^ *(_DWORD *)(a2 + 4i64 * (v7 ^ i & 3))) + (v12 ^ v10)) ^ (((16 * v11) ^ (v12 >> 3))
                                                                           + ((4 * v12) ^ (v11 >> 5))));
      *(_DWORD *)(*(_QWORD *)&v15[4] + 4i64 * i) = v3;
      v11 = v3;
    }
    v4 = **(_QWORD **)&v15[4] == 0xEi64;
    **(_QWORD **)&v15[4] ^= 0xEui64;
    if ( v4 )
    {
      v2 = *(_QWORD *)v15;
      **(_QWORD **)&v15[4] += *(_QWORD *)v15;
    }
    **(_QWORD **)&v15[4] ^= v2;
    v5 = *(_DWORD *)(*(_QWORD *)&v15[4] + 56i64)
       + (((v11 ^ *(_DWORD *)(a2 + 4i64 * (v7 ^ i & 3))) + (**(_DWORD **)&v15[4] ^ v10)) ^ (((16 * v11) ^ (**(_DWORD **)&v15[4] >> 3))
                                                                                          + ((4 * **(_DWORD **)&v15[4]) ^ (v11 >> 5))));
    *(_DWORD *)(*(_QWORD *)&v15[4] + 56i64) = v5;
    v11 = v5;
    --v8;
  }
  while ( v8 );
  v13 = 60;
  while ( v13 != 1 )
  {
    --v13;
    if ( *(unsigned __int8 *)(*(_QWORD *)&v15[4] + v13) != (byte_7FF7A5187000[v13 + 1] ^ 0x23) )
      return 0;
  }
  return 1;
}

这个的特征很明显是xxtea，并且没有魔改，网上直接搜脚本
exp：(需要用clang)
(网上的脚本https://www.cnblogs.com/zpchcbd/p/15974293.html)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <stdio.h>
#include <stdint.h>
#define DELTA 0x9e3779b9
#define MX (((z>>5^y<<2) + (y>>3^z<<4)) ^ ((sum^y) + (key[(p&3)^e] ^ z)))

void btea(uint32_t* v, int n, uint32_t const key[4])
{
	uint32_t y, z, sum;
	unsigned p, rounds, e;
	if (n > 1)            /* Coding Part */
	{
		rounds = 6 + 52 / n;
		sum = 0;
		z = v[n - 1];
		do
		{
			sum += DELTA;
			e = (sum >> 2) & 3;
			for (p = 0; p < n - 1; p++)
			{
				y = v[p + 1];
				z = v[p] += MX;
			}
			y = v[0];
			z = v[n - 1] += MX;
		} while (--rounds);
	}
	else if (n < -1)      /* Decoding Part */
	{
		n = -n;
		rounds = 6 + 52 / n;
		sum = rounds * DELTA;
		y = v[0];
		do
		{
			e = (sum >> 2) & 3;
			for (p = n - 1; p > 0; p--)
			{
				z = v[p - 1];
				y = v[p] -= MX;
			}
			z = v[n - 1];
			y = v[0] -= MX;
			sum -= DELTA;
		} while (--rounds);
	}
}


int main()
{
	unsigned char fakefalg[99] = { 0xff, 0xef, 0x79, 0xbc, 0xda, 0x6c, 0xc9,
						0xb1, 0x24, 0x90, 0x89, 0x5d, 0x99,
						0x42, 0xe1, 0x15, 0xc1, 0x1b, 0x2a,
						0x5a, 0x9f, 0x90, 0xe0, 0x5f, 0xe9,
						0x74, 0x9d, 0x44, 0x0d, 0x56, 0xfd,
						0x51, 0x7e, 0x34, 0x5a, 0xc5, 0x3a,
						0x5e, 0x24, 0xbc, 0xe1, 0x40, 0x0d,
						0x17, 0x68, 0xfc, 0xcc, 0x09, 0x5b,
						0xff, 0xc9, 0x45, 0x19, 0xb6, 0xc9,
						0x0a, 0x5e, 0xd9, 0x03, 0xb2, 0x48 };
	for (int i = 0; i < 61; ++i) {
		fakefalg[i] ^= 0x23;
	}
	uint32_t key[4] = { 0x1234,0x2341,0x3412,0x4123 };
	btea((unsigned*)(fakefalg + 1), -15, key);
	printf("解密后的数据：%s\n", (char*)fakefalg);
	return 0;
}

得到假flag：

1
DRKCTF{Sorry.There_is_no_more_flower_tea.Please_try_again!!}

很明显，这个不是真flag，这说明：
动态调试的时候和正常的时候运行的逻辑不一样
第一时间会想到这个可能是smc或者hook
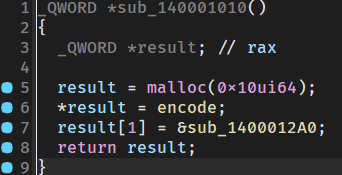
所以先查看encode的交叉引用。
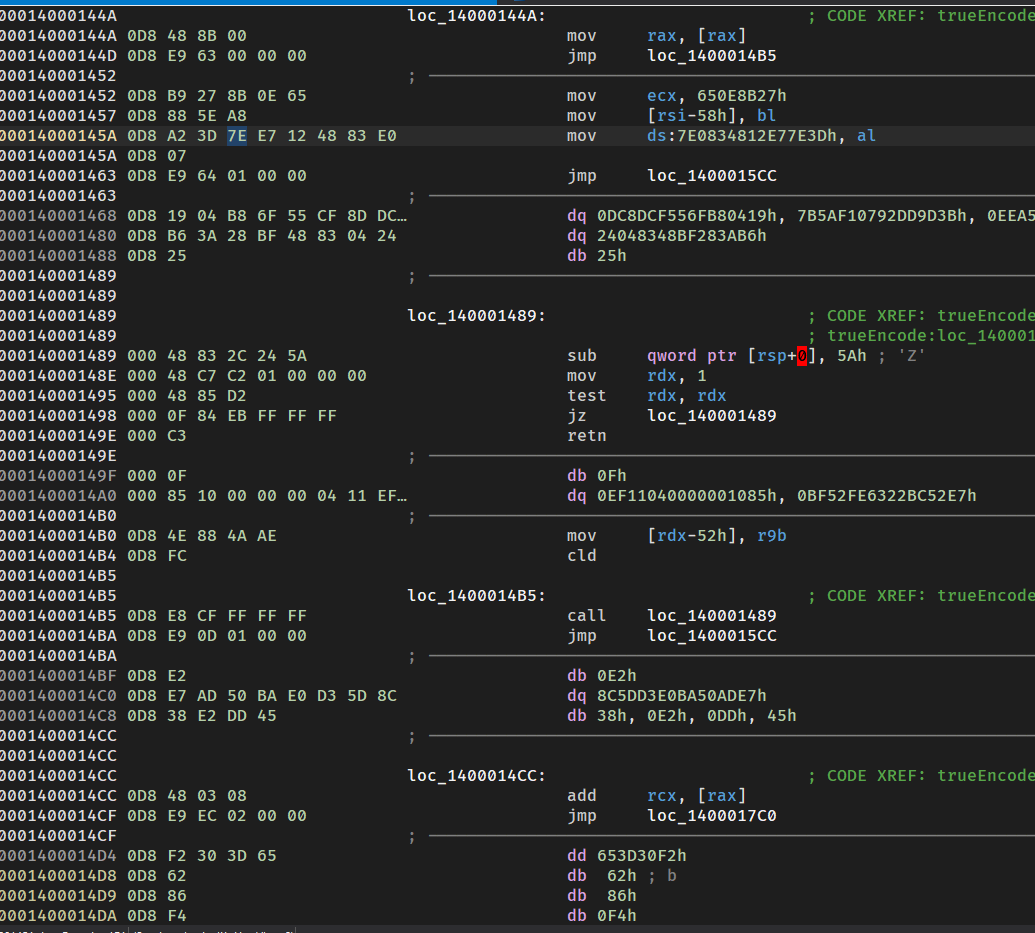
于是找到这个函数：
image.png
可以看到上层函数
修改了encode中的前几个字节用ret的方法返回到sub_140012A0中
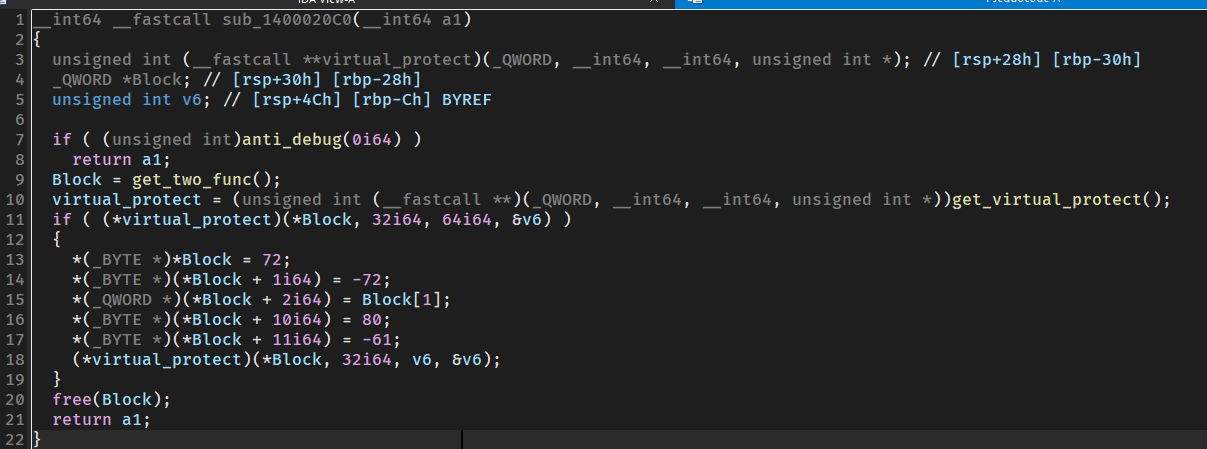
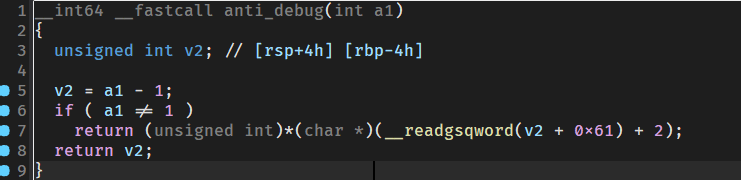
image.png
这里的第一个是反调试，在x64下，调试标志位在PEB表偏移0x2的位置，通过获取gs寄存器找到peb表的位置：
readsqword(0x62)得到调试标志位并判断当前进程是否在调试
image.png
block是单纯地得到对应的两个函数地址
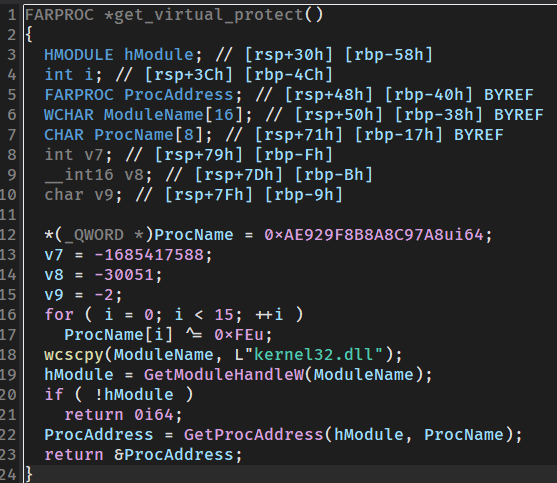
get_virtual_protect中，通过异或把virtualprotect函数名隐藏并通过搜索它在kernel32.dll中位置返回函数地址
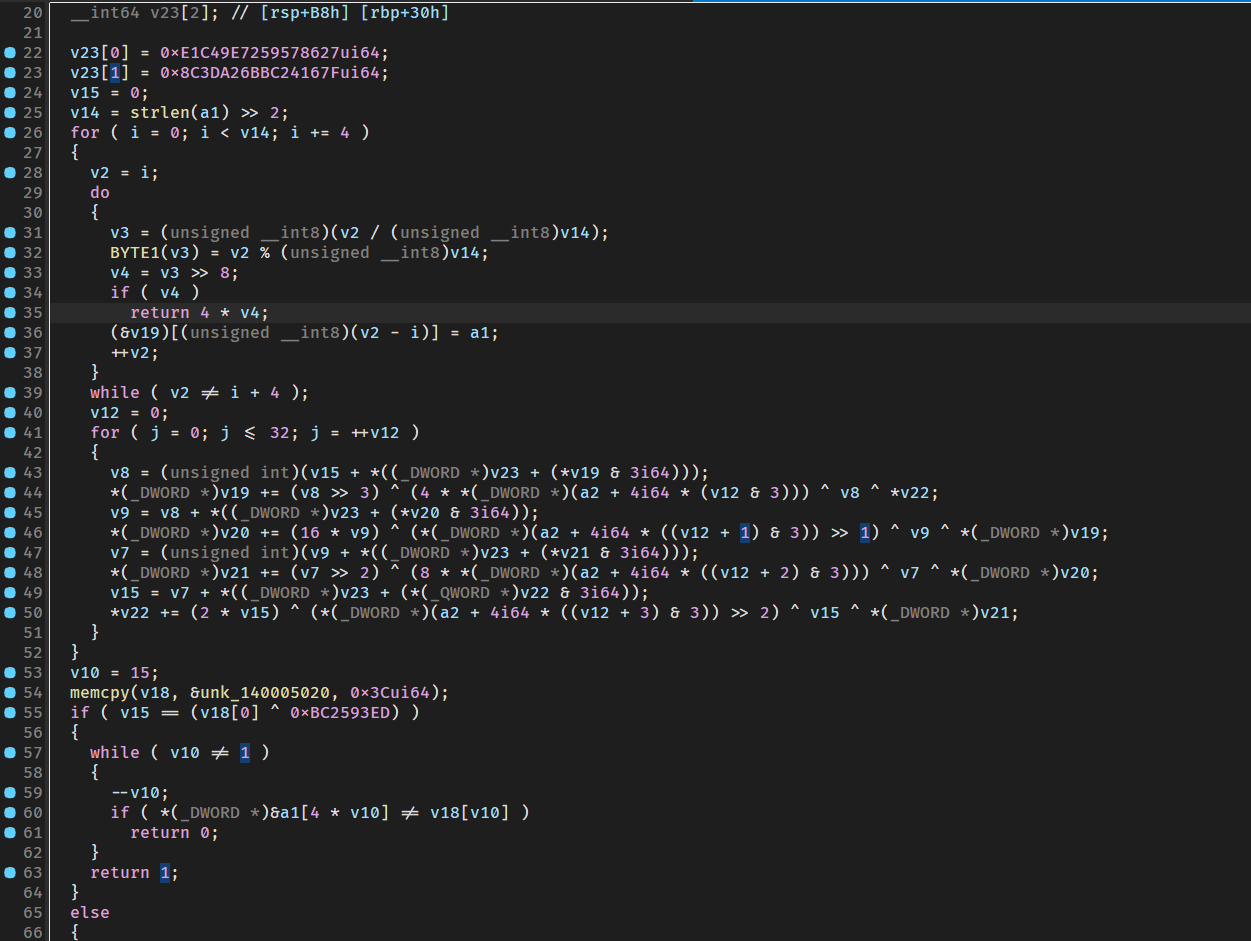
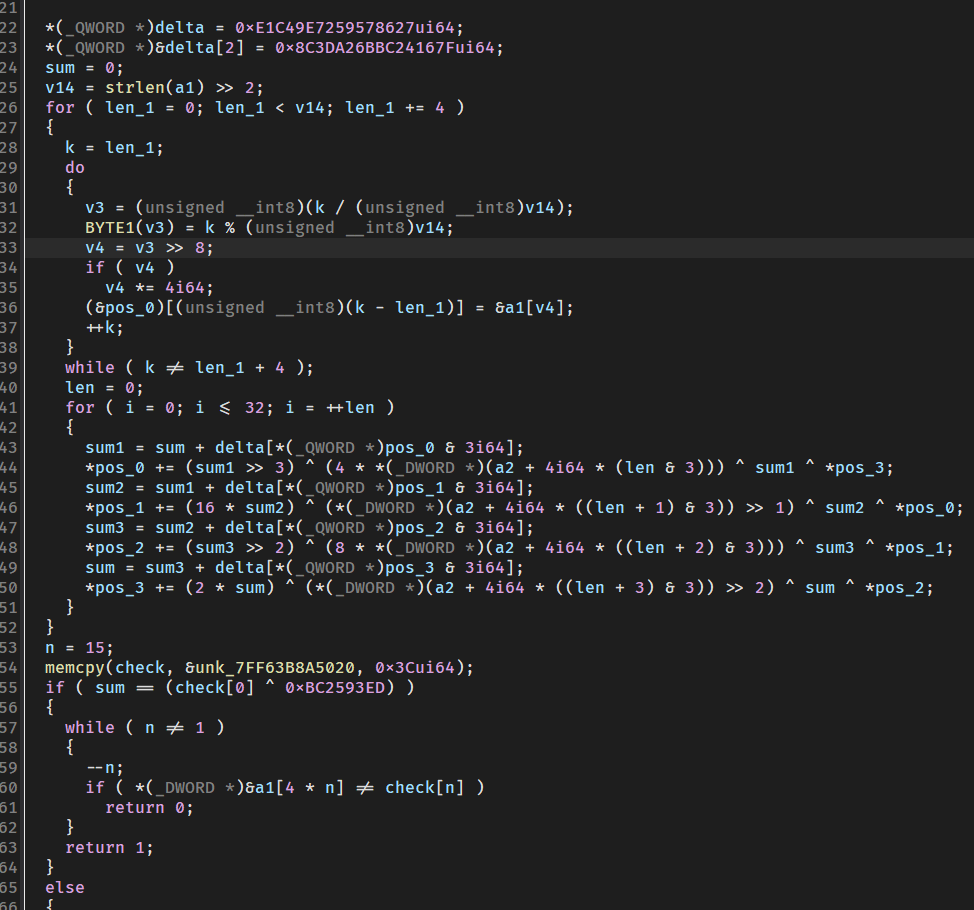
image.png
通过上面的分析，可以得出我们需要查看sub_140012A0的内容，这里才是真正的加密函数
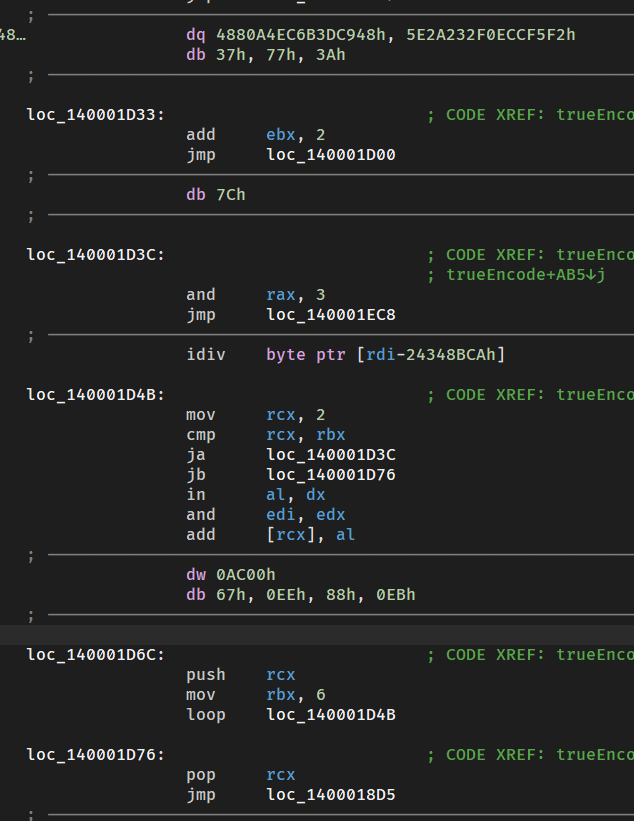
打开，还是花QAQ
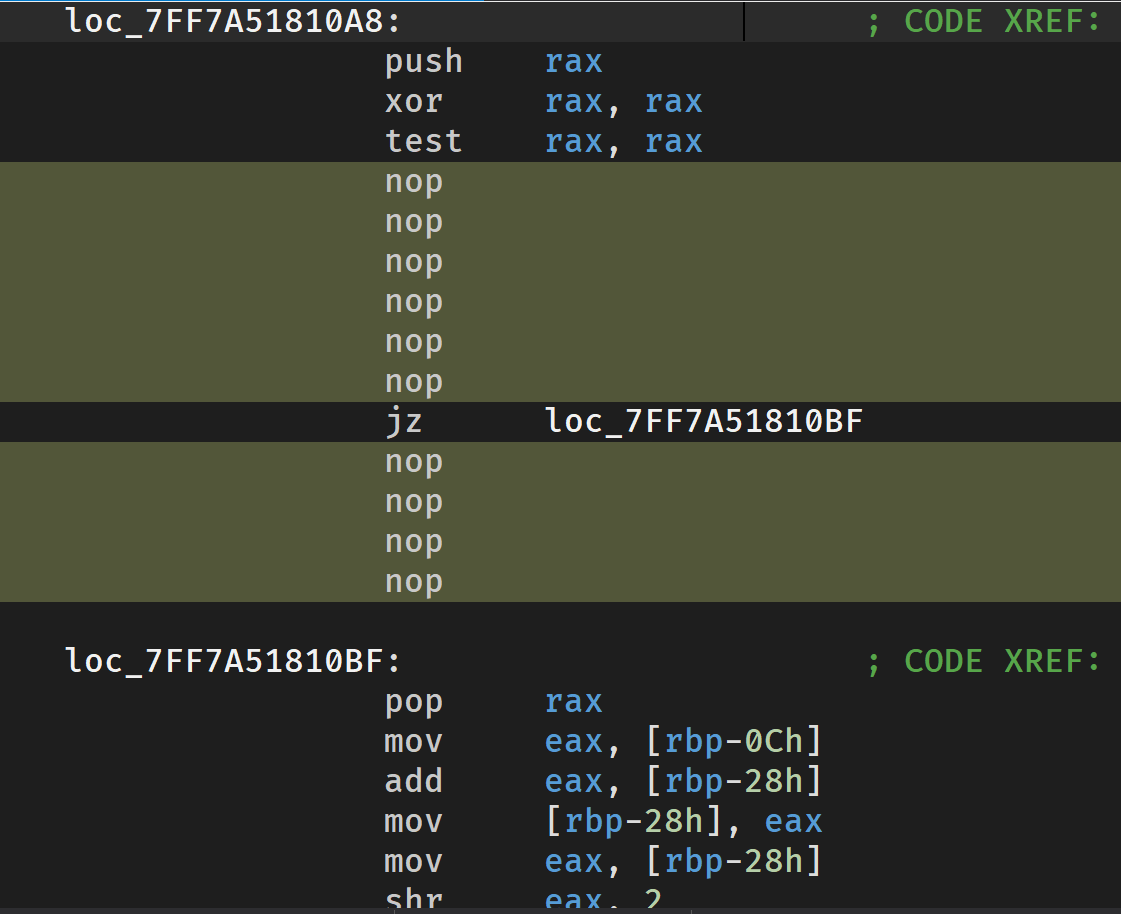
汇编中，可以看到函数后段全是一个指令+一个jmp
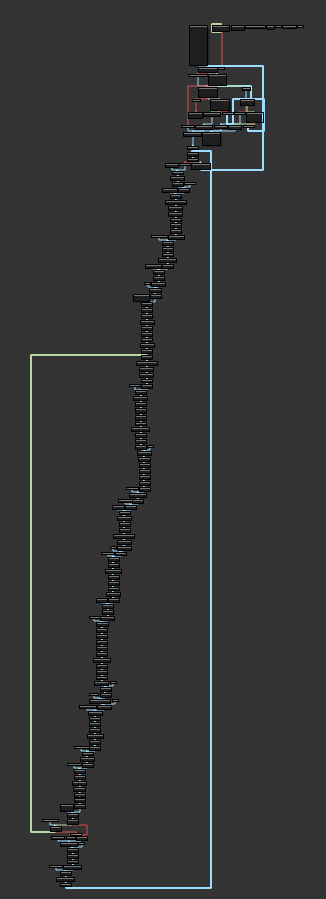
由于汇编不是很好看，改成流程图看奇怪的地方。
image.png
可以猜测：如果一个地方有一块代码，并且有连续jmp，这里可能是人工加的花
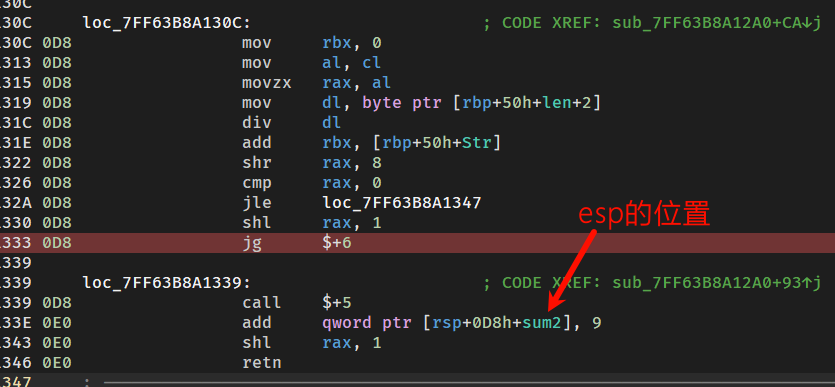
那么就先看一下那个很远的环和上面一排没有入口的块
1
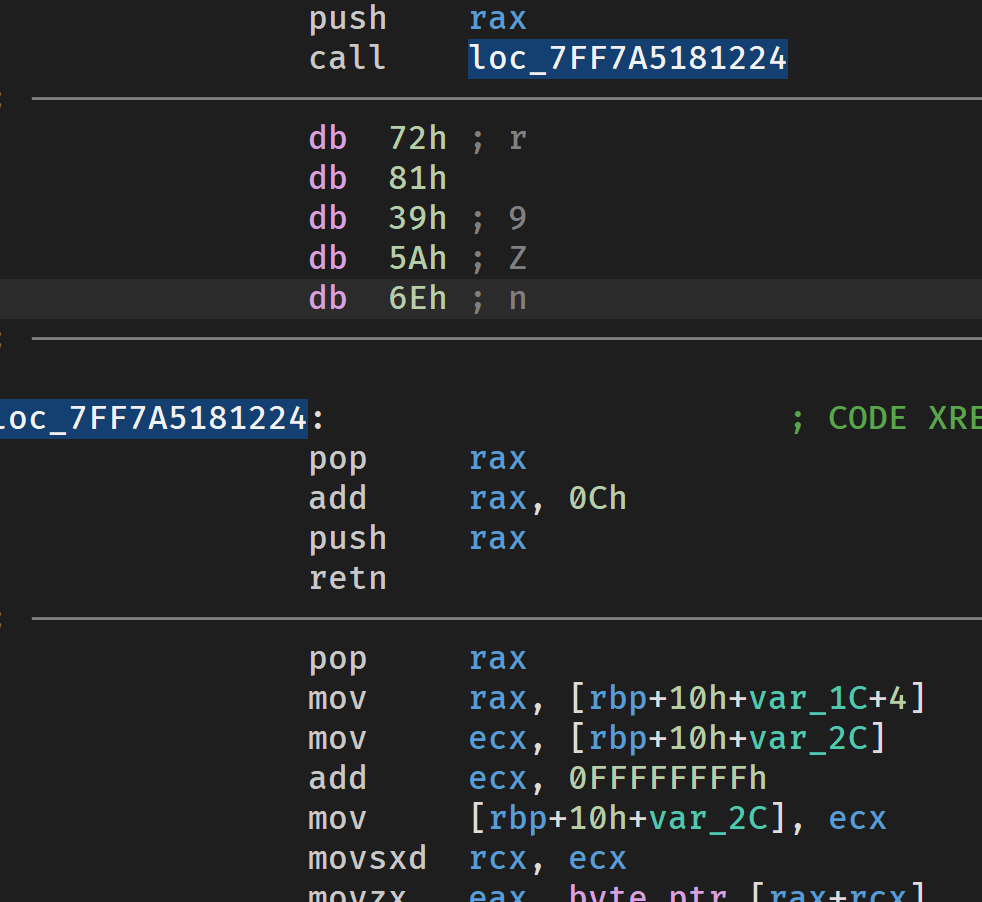
image.png
这里能看到push和pop，所以从push进入花，从pop离开花，可以看出可以这样还原
2
image.png
这里有一个call，尝试跟着call走，它下一步修改了返回地址，减去5A
即：140001460
转换一下这里的指令
image.png
所以把call nop了就好
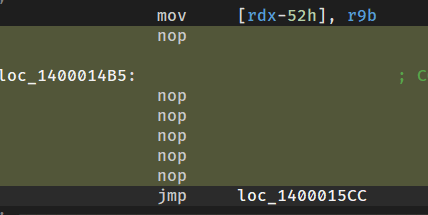
image.png
3
image.png
nop之后
然后全部u，c，p还原函数
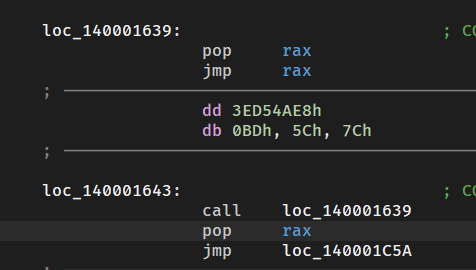
image.png
这里又可以看到上面的一个奇怪return，看汇编可以发现还是一个花
image.png
直接把call到retn去掉（除了shl）
这是一个变体tea，尝试化简这个函数
image.png
写脚本直接解
exp:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<stdio.h>
#include<fcntl.h>
#include<stdarg.h>
#include<stdint.h> 
#include<windows.h>


void dectrueTEA(uint32_t* flag, uint32_t* key, uint32_t E) {
	int i, j;
	const uint32_t delta[4] = { 0x59578627 ,0xe1c49e72,0xbc24167f ,0x8c3da26b };
	uint32_t e = E;
	const int len = 15;
	for (i = 0; i < len; i += 4) {
		uint32_t* c[4] = { &flag[(len - (i + 3)) % len],&flag[(len - (i + 2)) % len],&flag[(len - (i + 1)) % len],&flag[(len - i) % len] };
		for (j = 32; j >= 0; j--) {
			*c[3] -= ((e ^ *c[2]) ^ (key[(j + 3) % 4] >> 2)) ^ (e << 1);
			e -= delta[*c[3] % 4];

			*c[2] -= ((e ^ *c[1]) ^ (key[(j + 2) % 4] << 3)) ^ (e >> 2);
			e -= delta[*c[2] % 4];

			*c[1] -= ((e ^ *c[0]) ^ (key[(j + 1) % 4] >> 1)) ^ (e << 4);
			e -= delta[*c[1] % 4];

			*c[0] -= ((e ^ *c[3]) ^ (key[j % 4] << 2)) ^ (e >> 3);
			e -= delta[*c[0] % 4];
		}
		//printf("\n0x%x 0x%x 0x%x 0x%x\n", *c[0], *c[1], *c[2], *c[3]);
	}
	printf("%s", flag);
}


int main(void) {
	uint32_t E = 0;
	uint32_t k1[4] = { 0x1234,0x2341,0x3412,0x4123 };
	uint32_t a[] = { 0x127DC4E1, 0xCBA0EC0E, 0x570EDF5B, 0x99062A35, 0x382A7E1B, 0x15E46742, 0x4E5E456F, 0x3834C1D6, 0x5EF778A5, 0xAF217212, 0xC2D79D20, 0xD5C5935F, 0xCD2F5BB, 0xC527398C, 0x5EAC6739 };
	E = 0xAE58570C;
	dectrueTEA(a, k1, E);
	return 0;
}

Debug

die看不出来壳，但是ida可以，所以用x64dbg到脱完壳的地方，

不过得先调试，结果用ida调试直接寄在tls的call rax里面，用x64dbg一点事都没有，百思不得其解，最后发现

image-20240529215820329

tls里面有个反调试，在解壳之前，所以得先跳过，dbg里面自带的插件直接秒了，所以dbg就没事QAQ

这个感觉很不错，要是有办法在ida里面用就好了

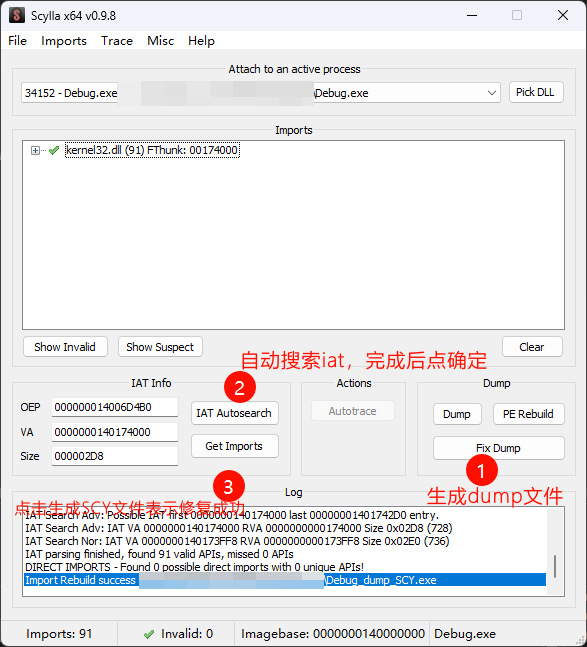
记录一下用工具修复iat表的过程：

x64dbg 插件 scylla

image-20240529205550754

去反调试，然后把smc搞出来，直接解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from prism import *
flag = ''
last = [0xCF, 0xD9, 0xC0, 0xC8, 0xDF, 0xCD, 0x0C, 0xD2, 0x43, 0x98, 0x10, 0xC0, 0x83, 0x43, 0x9A, 0x10, 0xCD, 0x42, 0x8C, 0x4A, 0x10, 0xC8, 0x82, 0x83, 0x4A, 0x9F, 0x8C, 0xDF, 0x98, 0x42, 0x8C, 0xDF, 0x84, 0x82, 0x83, 0x46, 0x52, 0x52, 0x52,0xE]
for len in range(40):
    for c in range(32,127):
        k = c
        if c <=0x40 or c>=0x5b:
            if c<=0x60 or c >= 0x7b:
                c-=30
                c^=0x51
            else:
                c-=32
                c^=0xcd
        else:
            c+=32
            c^=0xab
        if c==last[len]:
            flag+=chr(k)
            break
print(flag)
#DRKCTF{Y0u_Kn0w_F1a9_Con9raTu1aTion5!!!}

一起做杯下午茶吧

不会QAQ

Osint

羡慕群友每一天

直接开搜

image-20240527145103522

发现不是中间圆心的位置好像不一样

找另一个

1
DRKCTF{美国-弗罗里达州-迈阿密-Skyviews}
1
DRKCTF{美国-佛罗⾥达州-迈阿密-Skyviews}
1
DRKCTF{美国-佛罗里达州-迈阿密-Skyviews}
1
DRKCTF{美国-佛罗里达州-迈阿密州-Skyviews}
1
DRKCTF{美国-佛罗里达州-迈阿密市-Skyviews}

第五个是对的

Misc

DNA -5

提示：遥遥领先

抽象的题，没看wp之前我绝对想不到QAQ

1
ACGCTAATACCATCAACTCCATAACTCCCCACCTAAATCCAATAACCAGCTAAATCCAATAACCACTACCCCTCCATAAGAGAATAACCACTCATCCCCCTAATAAGAATAAACCTCCCCCAC

根据wp，由遥遥领先想到5G，又因为-5，所以可以想到要少5个G

1
ACCTAATACCATCAACTCCATAACTCCCCACCTAAATCCAATAACCACTAAATCCAATAACCACTACCCCTCCATAAAAATAACCACTCATCCCCCTAATAAAATAAACCTCCCCCAC

看这个可以先试试DNA解密

不行

结果是摩斯

1
2
WIPXGU%u7bSZ_SZ_1G5_N0IH3%u7d
WIPXGU{SZ_SZ_1G5_N0IH3}

然后解atbash

1
DRKCTF{HA_HA_1T5_M0RS3}